En el mundo de la computación cuántica, comprender los parámetros hamiltonianos de un sistema se ha vuelto crucial para avanzar en las capacidades de las tecnologías de simulación cuántica. Un grupo de investigadores de la Freie Universität Berlín, la Universidad de Maryland, el NIST, Google AI y Abu Dabi han emprendido un viaje innovador para abordar este desafío fundamental, refinando técnicas que prometen mejorar la precisión de las simulaciones cuánticas. Su trabajo podría allanar el camino hacia sistemas cuánticos que superen los límites computacionales clásicos, una fascinante frontera en la mecánica cuántica.
Esta compleja travesía comenzó con una llamada inesperada durante una conferencia en Brasil. Jens Eisert, el autor principal del artículo reciente de los investigadores, fue contactado por colegas que enfrentaban obstáculos significativos en la calibración del chip cuántico superconducting Sycamore utilizando metodologías de aprendizaje hamiltoniano. Inicialmente, el problema parecía sencillo, pero pronto Eisert descubrió que recuperar con precisión las frecuencias del operador hamiltoniano era una tarea más intrincada de lo anticipado.
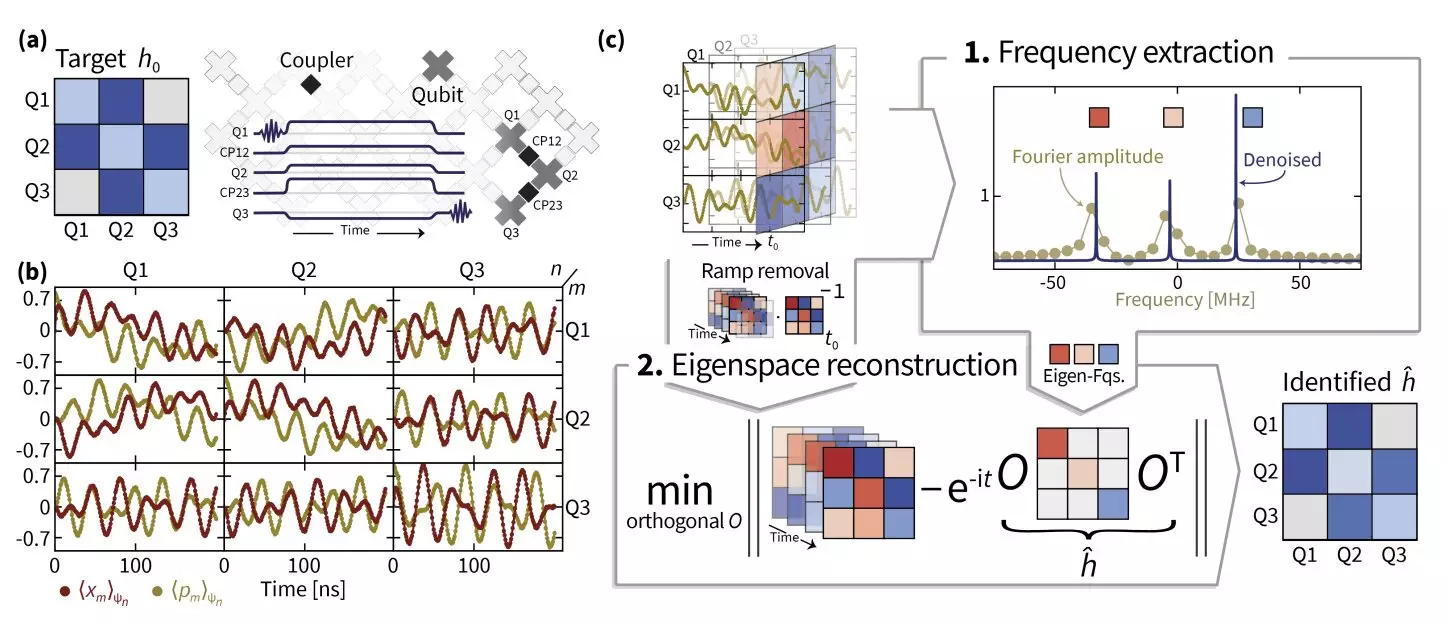
Confrontado con esta complejidad, Eisert invitó a dos excepcionales estudiantes de doctorado, Ingo Roth y Dominik Hangleiter, a aportar su experiencia. Juntos, abordaron los problemas subyacentes con vigor. Su idea inicial de aplicar técnicas de super-resolución emergió como una solución potencial, pero los datos del mundo real presentaron nuevos desafíos que requirieron años de investigación y esfuerzo de desarrollo dedicados para resolver. Al emplear la super-resolución, los investigadores pudieron mejorar la estimación de valores propios, crucial para identificar con precisión las frecuencias hamiltonianas.
Además, incorporaron la optimización de variedades, un enfoque algorítmico sofisticado diseñado para problemas complejos donde las variables se encuentran sobre un manifold curvado en lugar de un espacio euclidiano estándar. Este método facilitó la recuperación de espacios propios correspondientes al operador hamiltoniano, proporcionando el marco esencial necesario para determinar hamiltonianos desconocidos a partir de datos limitados.
Eisert subrayó la importancia de comprender las características no ideales de los interruptores cuánticos; estos no eran instantáneos y, en ocasiones, no eran unitarios. Las discrepancias al intentar ajustar una evolución hamiltoniana, cuando se acoplaban con procesos de conmutación defectuosos, resultaban en salidas caóticas. La introducción de TensorEsprit, su nuevo método de procesamiento de señales, surgió como un avance significativo, permitiendo la recuperación robusta de parámetros hamiltonianos, incluso en sistemas de considerable complejidad.
La combinación de super-resolución y optimización de variedades condujo a logros notables para el equipo de investigación. Sus metodologías identificaron con éxito los parámetros hamiltonianos en sistemas de hasta 14 qubits superconductores acoplados en dos procesadores Sycamore. Eisert señaló una realización crítica durante el proyecto: para recuperar con precisión los espacios propios, se deben poseer valores propios extremadamente precisos. Esta revelación aclaró por qué hay relativamente pocos estudios dedicados al aprendizaje hamiltoniano; el proceso está plagado de dificultades prácticas.
Los hallazgos iniciales sugirieron que las técnicas desarrolladas poseen escalabilidad y aplicabilidad para procesadores cuánticos extensos, insinuando implicaciones más amplias para la caracterización de parámetros hamiltonianos en sistemas cuánticos.
A medida que se preparaban para tomar los siguientes pasos, los investigadores anticiparon con entusiasmo la aplicación de sus métodos para explorar la dinámica de sistemas cuánticos interactuantes y estudiar sistemas atómicos fríos a través de metodologías inspiradas en redes tensoriales. Eisert sostiene que una comprensión más profunda de los hamiltonianos podría convertirse en algo primordial en el campo de la mecánica cuántica.
Tradicionalmente, se presume que el hamiltoniano de un sistema es conocido; sin embargo, esta suposición puede ser engañosa. La esencia de los experimentos cuánticos radica en su dependencia de los datos. Las capacidades predictivas de los sistemas cuánticos dependen por completo de una comprensión precisa del hamiltoniano.
El trabajo continuo de los investigadores tiene como objetivo no solo aclarar la comprensión de los operadores hamiltonianos, sino también informar sobre los avances en tecnologías cuánticas. Al mejorar la caracterización de simuladores cuánticos analógicos, sus esfuerzos podrían desbloquear nuevos caminos hacia la construcción de simulaciones cuánticas de alta precisión. Como afirmación de Eisert, la simulación cuántica analógica tiene el potencial de revolucionar la exploración de sistemas cuánticos intricados, permitiendo a los investigadores recrear y estudiar estos fenómenos bajo condiciones de laboratorio meticulosamente controladas.
La iniciativa emprendida por los investigadores simboliza un gran avance en la conexión de conceptos teóricos y aplicaciones experimentales en mecánica cuántica. Al abordar y superar los desafíos asociados con la estimación de parámetros hamiltonianos, están sentando las bases para futuras tecnologías y simulaciones cuánticas. Esta intersección de métodos innovadores y aplicaciones prácticas promete desbloquear nuevas dimensiones en la investigación cuántica, avanzando nuestro entendimiento del mundo cuántico y sus posibles aplicaciones en diversos campos científicos. A medida que la comunidad investigadora continúa lidiando con las complejidades de la dinámica cuántica, las ideas obtenidas de este trabajo podrían pronto iluminar nuevos caminos hacia lograr una precisión sin precedentes en las simulaciones cuánticas.

Deja una respuesta